Part I: AVL Trees
The following questions are in regards to AVL Trees. If you have't done the reading for this chapter, I suggest skipping Part I and attempting Part II.
Question 1
What is the relationship between the balance factor of a node and the height
of the node's children?
Question 2
What is the relationship between the balance factor and the direction of
rotation when rebalancing?
The following questions are in regard to the AVL Tree below.
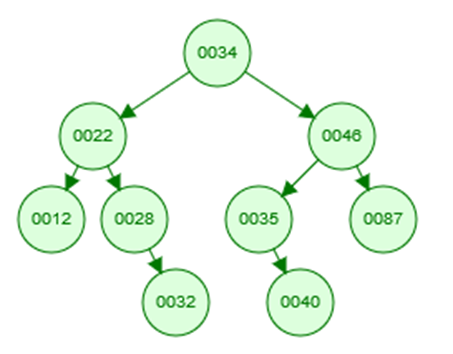
Question 3
Mark the height and balance factor for each node.
Question 4
What does the tree look like after the following operations? Be sure to
draw the relevant sections of the tree after each operation.
tree.insert(33);
tree.insert(26);
tree.insert(37);
tree.insert(39);
Use the following site to verify your AVL Trees: [Click me!][AVLCheck]
Part II: 2-3 Trees
2-3 Trees are trees that have properties that keep it balanced and ordered. The benefit of this
is that traversal algorithms will always have a worst case runtime of O(log(n)). Unlike a generic
tree, this tree will never end up looking like a diagonal linked list. This is great if you have
a lot of data and want to search through it quicikly!
Some properties include:
- All leaves are always on the same level (bottom)
- Each node can have up to 2 values and up to 3 children
- There can not exist a parent with only 1 child (unbalanced)
Insertion Exercises
Here is a BST that had the numbers 39 through 32 inserted.
redraw the tree without the gray insertions and reinsert 39 through 32 (in descending order)
as a 2-3 tree.
Hint 1: After inserting 36, the root should have 2 values and 3 children.
Hint 2: After inserting 32, the tree should have a height of 3.
Deleting Exercises
Now try deleting 100 from the following tree!
Try it with strings!
